Rotaciones
Las rotaciones, son aquellas isometrías que permiten girar todos los puntos del plano. Cada punto gira siguiendo un arco que tiene un centro y un ángulo bien determinados, por lo que toda rotación queda definida por su centro de rotación y por su ángulo de giro. Si la rotación se efectúa en sentido contrario a como giran las agujas del reloj, se dice que la rotación es positiva o antihoraria; en cambio si giran en el mismo sentido que las agujas del relo, se dice que la rotación es negativa u horaria.
Observaciones
Una rotación con centro O y ángulo de giro α , se representa por R O, α .
En este applet pueden ver cómo varía un punto al rotarlo desde un centro fijo con diferentes ángulos y sentidos Rotacion

Traslación y rotación

Traslación: Isometría en que todos los puntos se desplazan una distancia fija, con una dirección constante y un sentido dado, es decir con un VECTOR determinado.
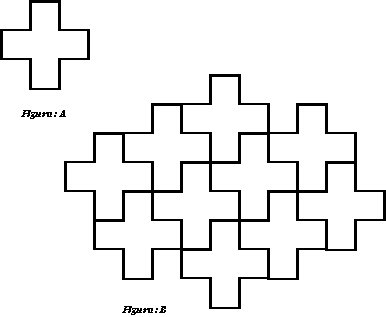
Los dibujos que están aquí son ejemplos de traslaciones.

Los trabajadores de la construcción hacen paredes y suelos montando grandes cantidades de cuerpos sólidos geométricos, la mayoría de las veces, idénticos. Muchas aceras, calzadas, zócalos, frisos e incluso paredes completas se hacen con losetas de diferentes tamaños, formas y unidas entre sí en distintas posiciones.

A las losetas que cubren una superficie plana y se ajustan bien entre sí, sin dejar huecos ni montarse unas encima de otras, se les llaman teselas. Cuando una superficie se puede cubrir perfectamente en todas las direcciones con este tipo de losetas o teselas, decimos que hemos realizado una teselación o traslación.

La figura A es un pentominó, con ella podemos rellenar el plano, es decir, podemos hacer una traslación -figura B-. Observen que no deja huecos ni se monta una sobre otra.

Utilizando los polígonos regulares que se dan, investigar cuál o cuáles de ellos pueden ponerse alrededor de un vértice sin que dejen huecos ni se monten unos encima de otros.

Combinando más de un polígono regular, construir distintas traslaciones.

Les dejo aquí un link donde podrán encontrar evaluaciones para hacer on line y algunos juegos relacionados TRASLACION