Rotaciones
Las rotaciones, son aquellas isometrías que permiten girar todos los puntos del plano. Cada punto gira siguiendo un arco que tiene un centro y un ángulo bien determinados, por lo que toda rotación queda definida por su centro de rotación y por su ángulo de giro. Si la rotación se efectúa en sentido contrario a como giran las agujas del reloj, se dice que la rotación es positiva o antihoraria; en cambio si giran en el mismo sentido que las agujas del relo, se dice que la rotación es negativa u horaria.
Observaciones
Una rotación con centro O y ángulo de giro α , se representa por R O, α .
En este applet pueden ver cómo varía un punto al rotarlo desde un centro fijo con diferentes ángulos y sentidos Rotacion
jueves, 13 de octubre de 2011
miércoles, 12 de octubre de 2011
Traslación y rotación
Traslación: Isometría en que todos los puntos se desplazan una distancia fija, con una dirección constante y un sentido dado, es decir con un VECTOR determinado.
Los dibujos que están aquí son ejemplos de traslaciones.Los trabajadores de la construcción hacen paredes y suelos montando grandes cantidades de cuerpos sólidos geométricos, la mayoría de las veces, idénticos. Muchas aceras, calzadas, zócalos, frisos e incluso paredes completas se hacen con losetas de diferentes tamaños, formas y unidas entre sí en distintas posiciones.
A las losetas que cubren una superficie plana y se ajustan bien entre sí, sin dejar huecos ni montarse unas encima de otras, se les llaman teselas. Cuando una superficie se puede cubrir perfectamente en todas las direcciones con este tipo de losetas o teselas, decimos que hemos realizado una teselación o traslación.
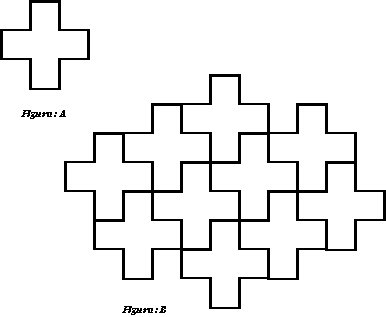
La figura A es un pentominó, con ella podemos rellenar el plano, es decir, podemos hacer una traslación -figura B-. Observen que no deja huecos ni se monta una sobre otra.
Utilizando los polígonos regulares que se dan, investigar cuál o cuáles de ellos pueden ponerse alrededor de un vértice sin que dejen huecos ni se monten unos encima de otros.
Combinando más de un polígono regular, construir distintas traslaciones.
Les dejo aquí un link donde podrán encontrar evaluaciones para hacer on line y algunos juegos relacionados TRASLACION
martes, 23 de agosto de 2011
COMENZAMOS CON GEOMETRÍA
Aquí les dejo un breve test a modo de repaso del año anterior, a ver que recuerdan!
Entren aquí para verlo e imprimirlo: Geometría
Y otro más de cuadriláteros: Cuadriláteros
Entren aquí para verlo e imprimirlo: Geometría
Y otro más de cuadriláteros: Cuadriláteros
miércoles, 27 de julio de 2011
Llegamos a la mitad del curso y se empiezan a complicar un poquito las cosas!A estudiar más, a participar más!
A partir de ahora comenzamos con un tema nuevo y continuamos reafirmando todo lo dado hasta ahora.
Prometo subir en estos días los clip de sonido que grabamos con el rap. Recuerden la letra, así tiene claras las reglas y no se equivocan al operar.
Les dejo entonces algunos de los ejercicios vistos en clase sobre probabilidad y si alguien quiere subir los resultados de las encuestas, Bienvenido!
Probabilidad
Ejercicio nº 1.-
a) Encuentra la probabilidad de
A = "Obtener par" B = "Obtener impar
C = "Obtener primo" D = "Obtener impar menor que 9
Ayuda
(escribiendo todos sus elementos).A= {2, 4, 6, 8, 10, 12, 14, 16}
B= {3, 5, 7, 9, 11, 13, 15}
C = {2, 3, 5, 7, 11, 13}
Ejercicio nº 2.-
Extraemos una carta de un mazo de cartas españolas (de cuarenta cartas). Calcula la probabilidad de que sea:
a) De oros. b) Una figura (rey, sota o caballo).
c) Un número menor que 5. d) Un rey.
miércoles, 15 de junio de 2011
EL RAP DE LAS ECUACIONES
No me la compliques
porque yo quiero aprender
si queres que haga el esfuerzo
ayudamelo a entender
SUMAS ALGEBRAICAS
sumas algebraica
de signos diferentes
resto al mayor
el menor: es evidente
aprender lo de los signo
porque es muy importante
y hay que a_tenderlo bien
para no e_quivocarte
el mayor de los valores
lo determinará
si el mayor es negativo
signo menos lo será
si tenias menos cuatro
sumandole 22
es 18 positivo (-4+22=+18)
no hay problema en estos dos
y si tengo -30
sumandole 23
me da siete negativo (-30+23=-7)
revisalo ¿lo entendes?
No me la compliques
porque yo quiero aprender
si queres que haga el esfuerzo
ayudamelo a entender
REGLA DE LOS SIGNOS:
Mas por menos menos
menos por menos mas
menos por mas menos
mas por mas mas
Cuando estoy multiplicando
numeros que tienen signo
uso reglas conocidas
que repetire aqui mismo
recorda que dividiendo
es como multiplicando
y que en un error de signo
las cosas no te estan dando
REGLA DE LOS SIGNOS:
Mas por menos menos
menos por menos mas
menos por mas menos
mas por mas mas
VARIABLES!
Esas letras misteriosas
que el profe llama variables
van cambiando en cada paso
no sabemos cuanto valen
parecido a una alcancia
con contador de dinero
el contenido varía
cuanto vale no sabemos
No me la compliques
porque yo quiero aprender
si queres que haga el esfuerzo
ayudamelo a entender
expresiones algebraica
son varias operaciones
entre numeros, variables
formulas, y hasta ecuaciones
ecuacion una igualdad
que tiene dos componentes
de la izquierda a la derecha
la igualdad aqui no miente
REGLA DE LOS SIGNOS:
Mas por menos menos
menos por menos mas
menos por mas menos
mas por mas mas
Cuando veo una ecuacion
que parece un baja y sube
distribuyo bien el peso
que no se vaya a las nubes
expresiones algebraicas
colocamos a los lados
realizas operaciones
manteniendo lo igualado
No me la compliques
porque yo quiero aprender
si queres que haga el esfuerzo
ayudamelo a entender
despejar es simplemente
dejar sola a una variable
lo que saco de este miembro
hacia el otro lado sale
varias reglas para hacerlo
deberemos respetar
nada se desaparece
mantenemos la igualdad
No me la compliques
porque yo quiero aprender
si queres que haga el esfuerzo
ayudamelo a entender
podemos sumar, restar
expresiones o valores
multiplico, dividir
potencias, radicaciones
pero si sumo a la izquierda
tambien lo hago a la derecha
operando en ambos lados
algunas cuentas se mechan
si quiero multiplicar
para dejar X libre
debere hacer lo mismo
solucion es lo que sigue
REGLA DE LOS SIGNOS:
Mas por menos menos
menos por menos mas
menos por mas menos
mas por mas mas
REGLA DE pasaje
cuando sumo, cuando resto
debo hacerlo en ambos lados
para que no se nos cambie
lo que ya tengo igualado
de igual forma lo razono:
cuando estoy multiplicando
asi aumentara los mismo
expresiones de dos bandos
si tengo que dividir
debo dividirlo todo
sin dejar nada de lado
sigue igual de todos modos
No me la compliques
porque yo quiero aprender
si queres que haga el esfuerzo
ayudamelo a entender
4X menos 5
por ejemplo igual a 15 (4X-5=15)
sumo de los lados 5
y atiendo porque lo hice (4x-5+5=15+5)
deje solo al 4x
a la izquierda se ha quedado (4x=20)
tengo 20 a la derecha
porque ya lo he sumando
finalmente los divido (4X/4=20/4)
los dos miembros entre cuatro
asi dejo sola a x
divido veinte entre cuatro (X=5)
No me la compliques
porque yo quiero aprender
si queres que haga el esfuerzo
ayudamelo a entender
No me la compliques
porque yo quiero aprender
si queres que haga el esfuerzo
ayudamelo a entender
martes, 24 de mayo de 2011
QUE ES UNA FUNCIÓN?
¿Qué es una función?
Una función es como una máquina: tiene una entrada y una salida.
Y lo que sale está relacionado de alguna manera con lo que entra.
Ejemplos
"Multiplicar por 2" es una función muy simple
Nombres
Primero, es útil darle un nombre a una función. El nombre más común es "f", pero puedes ponerle otros como "g" ... o hasta "mermelada" si quieres.
Y también está bien darle nombre a lo que se va adentro de la función, se pone entre paréntesis () después del nombre de la función:
Así que f(x) te dice que la función se llama "f", y "x" se pone dentro
Y normalmente verás lo que la función hace a la entrada:
f(x) = 3x nos dice que la función "f" toma "x" y lo multiplica por 3.
Así que con la función "f(x) = 3x", una entrada de 4 da una salida de 12. De hecho podemos escribir f(4) = 12.
Relacionar
Arriba dije que una función es como una máquina. Pero una función no tiene engranajes ni correas ni partes que se muevan. ¡Y no destruye lo que pones dentro!
En realidad, una función relaciona la entrada con la salida.
Decir que "f(4) = 12" es como decir que 4 está relacionado de alguna manera con 12. O también 4 → 12
Ejemplo: este árbol crece 20 cm cada año, así que la altura del árbol está relacionada con la edad por la función a:
a(edad) = edad × 20
Así que si la edad es 10 años, la altura es a(10) = 200 cm
Volveremos a esta idea después de responder la pregunta...
¿Con qué tipo de cosas trabaja una función?
Los "números" parecen una respuesta clara, pero...
... ¿qué números? Por ejemplo, la función de la altura del árbol a(edad) = edad×20 no tiene sentido si la edad es menor que cero.
... también podrían ser letras ("A"→"B"), o códigos de identificación ("A6309"→"Acceso") o cosas más raras.
Una función es como una máquina: tiene una entrada y una salida.
Y lo que sale está relacionado de alguna manera con lo que entra.
Ejemplos
"Multiplicar por 2" es una función muy simple
Nombres
Primero, es útil darle un nombre a una función. El nombre más común es "f", pero puedes ponerle otros como "g" ... o hasta "mermelada" si quieres.
Y también está bien darle nombre a lo que se va adentro de la función, se pone entre paréntesis () después del nombre de la función:
Así que f(x) te dice que la función se llama "f", y "x" se pone dentro
Y normalmente verás lo que la función hace a la entrada:
f(x) = 3x nos dice que la función "f" toma "x" y lo multiplica por 3.
Así que con la función "f(x) = 3x", una entrada de 4 da una salida de 12. De hecho podemos escribir f(4) = 12.
Relacionar
Arriba dije que una función es como una máquina. Pero una función no tiene engranajes ni correas ni partes que se muevan. ¡Y no destruye lo que pones dentro!
En realidad, una función relaciona la entrada con la salida.
Decir que "f(4) = 12" es como decir que 4 está relacionado de alguna manera con 12. O también 4 → 12
Ejemplo: este árbol crece 20 cm cada año, así que la altura del árbol está relacionada con la edad por la función a:
a(edad) = edad × 20
Así que si la edad es 10 años, la altura es a(10) = 200 cm
Volveremos a esta idea después de responder la pregunta...
¿Con qué tipo de cosas trabaja una función?
Los "números" parecen una respuesta clara, pero...
... ¿qué números? Por ejemplo, la función de la altura del árbol a(edad) = edad×20 no tiene sentido si la edad es menor que cero.
... también podrían ser letras ("A"→"B"), o códigos de identificación ("A6309"→"Acceso") o cosas más raras.
sábado, 14 de mayo de 2011
DIVERTITE PENSANDO!
Como siempre, su profe pensando en uds, les deja aquí unos problemitas de pensar, con un poco de ingenio y creatividad salen, claro tambien con algo de matemáticas!Las palomas y las estacas
Llegaron las palomas y se posaron en estacas. Si en cada estaca se posa una paloma, hay una paloma que se queda sin estaca. Pero si en cada estaca se posan dos palomas, en una de las estacas no habrá paloma. ¿Cuántas eran las palomas? y, ¿cuántas las estacas?
Las hermanas y los hermanos
Yo tengo tantas hermanas como hermanos. Pero mi hermana tiene la mitad de hermanas que de hermanos. ¿Cuántos somos?
¿Cuántos años tienen?
-Dígame, usted, abuelo, ¿qué edad tiene su hijo?
-Tiene tantas semanas como mi nieto días,
-¿Y qué edad tiene su nieto?
-Tiene tantos meses como yo años.
-Entonces, ¿qué edad tiene usted?
-Los tres juntos tenemos exactamente 100 años. Ingéniate y sabrás qué edad tenemos cada uno.
¿Cuántas partidas?
Tres amigos jugaron a las damas. En total jugaron tres partidas. ¿Cuántas partidas jugó cada uno?
El caracol
Un caracol decidió subir a un árbol de 15 m de altura. Durante cada día tenía tiempo de subir 5 m; pero mientras dormía por la noche, bajaba 4 m.
¿Al cabo de cuántos días llegará a la cima del árbol?
Dos escolares
-Dame una manzana y tendré el doble que tú -le dijo un escolar a otro.
-Eso sería injusto. Es preferible que tú me des a mí una manzana, y entonces tendremos las mismas -le respondió su camarada.
¿Podrías decir cuántas manzanas tenía cada escolar?
sábado, 7 de mayo de 2011
Juegos matemáticos
1. Mira durante 40 segundos fijamente los cuatro puntos que están formando una línea vertical en el centro del dibujo.
2. Luego mira hacia otro lado y parpadea seguido sin parar.
¿Qué es lo que ves?
Mi cerebro es una máquina
Aqui les dejo un link a un juego que se relaciona con las ecuaciones de una forma divertida y en la que tienen que pensar rápido:
viernes, 6 de mayo de 2011
domingo, 1 de mayo de 2011
ECUACIONES
Bueno, comenzamos con un tema nuevo. aqui les dejo lo mas importante que estuvimos viendo en clase y espero que sigan haciendose seguidores y comenten lo que les parezca. Recuerden que este sitio esta hecho por y para uds. así que cualquier aporte que deseen hacer es bienvenido.
Una ecuación es una igualdad en la cual hay términos conocidos y términos desconocidos. El término desconocido se llama incógnita y se representa generalmente por las últimas letras del abecedario: “x”, “y” o “z”, aunque puede utilizarse cualquiera otra letra.
En estos ejemplos puede observarse lo siguiente:
Hay una expresión escrita a la izquierda del signo igual y hay una expresión escrita a la derecha del signo igual. La que está antes del signo igual recibe el nombre de primer miembro, la expresión que está a la derecha del signo igual se llama segundo miembro.
Les dejo como tarea pensar cuales pueden ser los valores de las tres primeas igualdades, lo pueden publicar como comentario, saludos a todos
viernes, 29 de abril de 2011
La ecuación como BALANZA
Resolución de ecuaciones
Una ecuación puede compararse con una balanza de platillos. Para mantener el perfecto equilibrio es necesario tener la misma masa en ambos lados. Si se aumenta la masa en el platillo de la izquierda, la balanza se inclinará hacia la izquierda, por lo tanto, para mantenerla equilibrada será necesario aumentar a la derecha la misma cantidad de masa.
Si, por el contrario, la masa disminuye, también habrá que disminuir la misma cantidad de masa en el otro platillo de la balanza.
Este ejemplo aplicado a una ecuación indica que si se agrega (suma) un número a la derecha, también es necesario sumar el mismo número a la izquierda para mantener la igualdad y si se resta, debe hacerse lo mismo a ambos lados. Lo mismo ocurre al multiplicar o dividir (Ver: Propiedades).
Debemos saber que existen ecuaciones de dos tipos: ecuaciones aditivas y ecuaciones multiplicativas.
· Las ecuaciones aditivas tienen la forma a + x = b
· Las ecuaciones multiplicativas tienen la forma a · x = b
1) Ecuaciones aditivas: a + x = b
Para resolver ecuaciones de la forma a + x = b se utiliza la Propiedad 1 antes mencionada; es decir, se usa la propiedad de las igualdades, que textualmente dice:
Cuando se suma o resta el mismo número en ambos miembros de una ecuación, la igualdad se mantiene.
Los pasos a seguir para encontrar la incógnita son los siguientes:
1. Se suma a ambos lados de la ecuación el opuesto del número que suma o resta a la incógnita. Recordar que el opuesto de un número es el mismo número con signo contrario (el opuesto de 6 es –6; el opuesto de –99 es 99. Recuerda además que +99 es lo mismo que 99).
2. Se realiza la operación indicada.
Ejemplo: 28 + x = 13
El número que acompaña a la incógnita sumándolo es 28, por lo tanto, se debe agregar a ambos lados de la ecuación su opuesto que es –28.
28 + x + –28 = 13 + –28
Como 28 y –28 tienen signo contrario entre sí, la regla de signos indica que deben restarse.
28 + –28 = 0
Como 13 y –28 son números de distinto signo, éstos se restan y se conserva el signo del número con mayor valor absoluto (el número sin signo).
13 + –28 = –15
Por lo tanto, después de realizar las operaciones indicadas más arriba, se tiene que:
28 + x = 13
28 + x +–28= 13 + –28
x + 0 = –15
x = –15
Otros ejemplos:
1) 60 – 37 = 84 + x
23 = 84 + x
23 + –84 = 84 + x + –84
–61 = 0 + x
x = –61
2) x + 3 – 2 = 7
x + 1 = 7
x + 1 + –1 = 7 + -1
x + 0 = 6
x = 6
2) Ecuaciones multiplicativas: a • x = b
Para resolver ecuaciones de la forma a · x = b se aplica la propiedad de las igualdades, que dice textualmente:
Si se multiplica o divide por un mismo número a ambos lados de la igualdad, ésta se mantiene.
Cuando se tiene una ecuación de esta forma, en la cual un número se halla multiplicando a la incógnita, se debe dividir a ambos lados de la ecuación por dicho número.
Los pasos son los siguientes:
1) Se divide siempre por el número que multiplica a la “x”.
Ejemplo: 15 • x = 75
tengo que divivdir a ambos miembros entre 15, entonces resulta 15 • x : 15 = 75 : 15
2) Se realizan las operaciones matemáticas correspondientes.
Reordenado los números se tiene: 15 : 15 • x = 75 : 15
1 • x = 5
x = 5
Otro ejemplo:
3 • x = 81
3 • x : 3 = 81 : 3
3 : 3 • x = 27
1 • x = 27
x = 27
¿Qué sucede si se combinan ambos tipos de ecuaciones: aditiva y multiplicativa ?
Ejemplo: 2x + 2 + 3 = 4x – 1
Para resolver este tipo de ecuación, lo primero que debe hacerse es efectuar las operaciones entre términos semejantes en ambos miembros de la ecuación; es decir, a la izquierda y a la derecha.
En este ejercicio esto significa sumar los números con los números y las “equis” con las “equis”. En el caso particular de nuestro ejemplo, a la izquierda se pueden sumar los números 2 y 3 solamente, pues no hay más términos semejantes
2x + 5 = 4x – 1
A continuación se debe sumar a ambos lados de la ecuación el opuesto del número que suma o resta a la incógnita, en este caso se debe sumar el opuesto de 5 (-5) a la izquierda y a la derecha de la igualdad.
2x + 5 + –5 = 4x - 1 + –5
2x + 0 = 4x + –6
2x = 4x + –6
Luego, debe sumarse el opuesto de 4x para lograr que el número 4x que está a la derecha quede a la izquierda de la ecuación; de esta forma los dos números con “equis” podrán reducirse.
2x = 4x + –6 / –4x
2x + –4x = 4x + –6 + –4x
– 2x = 4x + –4x + –6
– 2x = 0 + –6
– 2x = –6
Cuando se tiene una ecuación de esta forma, en la cual un número se halla multiplicando a la incógnita, se debe dividir a ambos lados de la ecuación por dicho número, en este caso se debe dividir por –2. Fíjate que la ecuación es ahora multiplicativa, por lo tanto se usa el método par resolver ecuaciones multiplicativas (por eso se divide por –2).
– 2x : –2 = –6 : –2
1x = 3
x = 3
Otro ejemplo:
5x – 3 = 2x + 6
1) Se suman o restan números con números y letras con letras en cada miembro de la ecuación. Como no hay términos semejantes en este caso, se continúa con el segundo paso.
5x – 3 + +3 = 2x + 6 + +3 / +3
5x + 0 = 2x + 9
2) Sumar el opuesto (sumar a ambos lados de la ecuación el número que resta o suma a la “x”)
5x = 2x + 9
Ahora falta sumar el opuesto de 2x (-2x)
5x + –2x = 2x + –2x + 9 /–2x
3x = 0 + 9
3x = 9
3) Dividir a ambos lados de la ecuación por el número que acompaña a la incógnita (3). Inverso multiplicativo.
3x ÷ 3 = 9 ÷ 3
3 ÷ 3x = 9 / 3 (Recuerda que el símbolo de división, ÷, también se puede representar como /).
x = 3
Nota: Todas las ecuaciones vistas hasta ahora son de Primer Grado (el exponente de la incógnita es 1) y pertenecen al Conjunto de los Números Enteros (los coeficientes numéricos son números positivos y negativos). Más adelante se estudiará la forma de resolver ecuaciones en el Conjunto de los Números Racionales.
Bueno, aqui les dejo la explicacion laarga sobre resolución de ecuaciones que nosotros vamos a utilizar luego en forma reducida, tal como lo empezamos a ver en estos dias. por favor léanla con detenimiento y sigan cada uno de los ejemplos, así evacúan dudas que puedan haber quedado.
Una ecuación puede compararse con una balanza de platillos. Para mantener el perfecto equilibrio es necesario tener la misma masa en ambos lados. Si se aumenta la masa en el platillo de la izquierda, la balanza se inclinará hacia la izquierda, por lo tanto, para mantenerla equilibrada será necesario aumentar a la derecha la misma cantidad de masa.
Si, por el contrario, la masa disminuye, también habrá que disminuir la misma cantidad de masa en el otro platillo de la balanza.
Este ejemplo aplicado a una ecuación indica que si se agrega (suma) un número a la derecha, también es necesario sumar el mismo número a la izquierda para mantener la igualdad y si se resta, debe hacerse lo mismo a ambos lados. Lo mismo ocurre al multiplicar o dividir (Ver: Propiedades).
Debemos saber que existen ecuaciones de dos tipos: ecuaciones aditivas y ecuaciones multiplicativas.
· Las ecuaciones aditivas tienen la forma a + x = b
· Las ecuaciones multiplicativas tienen la forma a · x = b
1) Ecuaciones aditivas: a + x = b
Para resolver ecuaciones de la forma a + x = b se utiliza la Propiedad 1 antes mencionada; es decir, se usa la propiedad de las igualdades, que textualmente dice:
Cuando se suma o resta el mismo número en ambos miembros de una ecuación, la igualdad se mantiene.
Los pasos a seguir para encontrar la incógnita son los siguientes:
1. Se suma a ambos lados de la ecuación el opuesto del número que suma o resta a la incógnita. Recordar que el opuesto de un número es el mismo número con signo contrario (el opuesto de 6 es –6; el opuesto de –99 es 99. Recuerda además que +99 es lo mismo que 99).
2. Se realiza la operación indicada.
Ejemplo: 28 + x = 13
El número que acompaña a la incógnita sumándolo es 28, por lo tanto, se debe agregar a ambos lados de la ecuación su opuesto que es –28.
28 + x + –28 = 13 + –28
Como 28 y –28 tienen signo contrario entre sí, la regla de signos indica que deben restarse.
28 + –28 = 0
Como 13 y –28 son números de distinto signo, éstos se restan y se conserva el signo del número con mayor valor absoluto (el número sin signo).
13 + –28 = –15
Por lo tanto, después de realizar las operaciones indicadas más arriba, se tiene que:
28 + x = 13
28 + x +–28= 13 + –28
x + 0 = –15
x = –15
Otros ejemplos:
1) 60 – 37 = 84 + x
23 = 84 + x
23 + –84 = 84 + x + –84
–61 = 0 + x
x = –61
2) x + 3 – 2 = 7
x + 1 = 7
x + 1 + –1 = 7 + -1
x + 0 = 6
x = 6
2) Ecuaciones multiplicativas: a • x = b
Para resolver ecuaciones de la forma a · x = b se aplica la propiedad de las igualdades, que dice textualmente:
Si se multiplica o divide por un mismo número a ambos lados de la igualdad, ésta se mantiene.
Cuando se tiene una ecuación de esta forma, en la cual un número se halla multiplicando a la incógnita, se debe dividir a ambos lados de la ecuación por dicho número.
Los pasos son los siguientes:
1) Se divide siempre por el número que multiplica a la “x”.
Ejemplo: 15 • x = 75
tengo que divivdir a ambos miembros entre 15, entonces resulta 15 • x : 15 = 75 : 15
2) Se realizan las operaciones matemáticas correspondientes.
Reordenado los números se tiene: 15 : 15 • x = 75 : 15
1 • x = 5
x = 5
Otro ejemplo:
3 • x = 81
3 • x : 3 = 81 : 3
3 : 3 • x = 27
1 • x = 27
x = 27
¿Qué sucede si se combinan ambos tipos de ecuaciones: aditiva y multiplicativa ?
Ejemplo: 2x + 2 + 3 = 4x – 1
Para resolver este tipo de ecuación, lo primero que debe hacerse es efectuar las operaciones entre términos semejantes en ambos miembros de la ecuación; es decir, a la izquierda y a la derecha.
En este ejercicio esto significa sumar los números con los números y las “equis” con las “equis”. En el caso particular de nuestro ejemplo, a la izquierda se pueden sumar los números 2 y 3 solamente, pues no hay más términos semejantes
2x + 5 = 4x – 1
A continuación se debe sumar a ambos lados de la ecuación el opuesto del número que suma o resta a la incógnita, en este caso se debe sumar el opuesto de 5 (-5) a la izquierda y a la derecha de la igualdad.
2x + 5 + –5 = 4x - 1 + –5
2x + 0 = 4x + –6
2x = 4x + –6
Luego, debe sumarse el opuesto de 4x para lograr que el número 4x que está a la derecha quede a la izquierda de la ecuación; de esta forma los dos números con “equis” podrán reducirse.
2x = 4x + –6 / –4x
2x + –4x = 4x + –6 + –4x
– 2x = 4x + –4x + –6
– 2x = 0 + –6
– 2x = –6
Cuando se tiene una ecuación de esta forma, en la cual un número se halla multiplicando a la incógnita, se debe dividir a ambos lados de la ecuación por dicho número, en este caso se debe dividir por –2. Fíjate que la ecuación es ahora multiplicativa, por lo tanto se usa el método par resolver ecuaciones multiplicativas (por eso se divide por –2).
– 2x : –2 = –6 : –2
1x = 3
x = 3
Otro ejemplo:
5x – 3 = 2x + 6
1) Se suman o restan números con números y letras con letras en cada miembro de la ecuación. Como no hay términos semejantes en este caso, se continúa con el segundo paso.
5x – 3 + +3 = 2x + 6 + +3 / +3
5x + 0 = 2x + 9
2) Sumar el opuesto (sumar a ambos lados de la ecuación el número que resta o suma a la “x”)
5x = 2x + 9
Ahora falta sumar el opuesto de 2x (-2x)
5x + –2x = 2x + –2x + 9 /–2x
3x = 0 + 9
3x = 9
3) Dividir a ambos lados de la ecuación por el número que acompaña a la incógnita (3). Inverso multiplicativo.
3x ÷ 3 = 9 ÷ 3
3 ÷ 3x = 9 / 3 (Recuerda que el símbolo de división, ÷, también se puede representar como /).
x = 3
Nota: Todas las ecuaciones vistas hasta ahora son de Primer Grado (el exponente de la incógnita es 1) y pertenecen al Conjunto de los Números Enteros (los coeficientes numéricos son números positivos y negativos). Más adelante se estudiará la forma de resolver ecuaciones en el Conjunto de los Números Racionales.
miércoles, 13 de abril de 2011
repasamos lo visto en clase
Estas últimas clases hemos dado por finalizada la revisión de 1er año para dar paso a los conceptos nuevos que nos tocan empezar a aprender.
Fuimos construyendo los conjuntos de números, desde los conocidos: Naturales, Enteros, hasta los Racionales y los Irracionales.
También nos familiarizamos con sus distintas expresiones, por ejemplo, sabemos que un racional es la expresion de una razón o cociente (o division, son todos sinónimos=) entre dos números enteros.
De esta division que escribimos como Numerador/Denominador podemos obtener dos posibles resultados: un Decimal Exacto ó un Decimal Periódico. Si pienso en sentido inverso cualquier número con esta forma se puede escribir como el cociente de dos enteros.( a este razonamiento se le llama recíproco)
Ejemplo
Cómo obtenemos la fracción correspondiente a un número decimal?
Los números 3,27 y 0,4235 se pueden escribir: 3,27= 327/100 y 0,4235=4235/10000
sucede que dividir entre 10, 100, 1000 o cualquier potencia de 10 implico, en los hechos, correr la coma hacia la izquierda uno, dos tres, o tantos lugares como ceros tenga el número.
completa el siguiente cuadro:
| Numero Decimal | Fraccion |
| 0,3 | |
| 5,42 | |
| -0,312 | |
| 0,83 | |
| -3,7 | |
| 2,138 | |
miércoles, 23 de marzo de 2011
MATEMATICAS DE SEGUNDO
Bienvenidos al curso de matemáticas de segundo, aqui tendremos un espacio para repasar lo visto en clase, aclarar dudas que puedan haber quedado y no se animaron a preguntar, ampliar un poco más lo dado para quienes tienen interes en ir más alla de lo trabajado en clase, en fin está abierto a todos para que participen y hagan las sugerencias que les surjan.
A medida que vayamos avanzando, aparecerán aqui los repartidos con ejercicios que uds deben hacer, deberes, resoluciones, tareas individuales o grupales, etc.
También trabajaremos con algunos sitios de la red, que nos permitirán hacer trabajos on line, tales como auto evaluaciones y juegos didácticos.
Bueno, estamos en contacto por medio de este espacio y quedo a las ordenes para cualquier consulta, les deseo un buen año a todos y los espero.
Prof. Elisa Bezerian
Aqui les dejo un link para que entren a una página con ejercicios y juegos muy interesantes, para que vayan comenzando a practicarse e investigar:
Jueduland
A medida que vayamos avanzando, aparecerán aqui los repartidos con ejercicios que uds deben hacer, deberes, resoluciones, tareas individuales o grupales, etc.
También trabajaremos con algunos sitios de la red, que nos permitirán hacer trabajos on line, tales como auto evaluaciones y juegos didácticos.
Bueno, estamos en contacto por medio de este espacio y quedo a las ordenes para cualquier consulta, les deseo un buen año a todos y los espero.
Prof. Elisa Bezerian
Aqui les dejo un link para que entren a una página con ejercicios y juegos muy interesantes, para que vayan comenzando a practicarse e investigar:
Jueduland
Suscribirse a:
Comentarios (Atom)